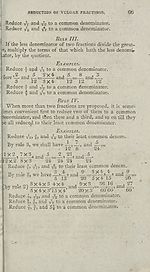Download files
Complete book:
Individual page:
Thumbnail gallery: Grid view | List view

62
REDUCTION OTF VULGAR FRACTIONS.
VI. Ti> reduce fractions of different denominators to equivc
lent fractions of a common one.
Rule I.
If the fractions can be conveniently reduced to a comma
denominator, by multiplying or dividing theif terms,
cording to note 6, page 57, proceed by that method ; bi
if not, multiply each numerator continually into all the d«
nominators, except its own, for each new numerator: an
multiply all the denominators together for the common d*
nominator.
Note. It is evident, that in this and several other operations, wh<
any ef the proposed quantities are integers, mixt numbers, or compoui
fractions, they must be reduced by their proper rules, to the form
simple fractions.
Examples.
Reduce |, f, and ^ to a common denominator.
Thus —» —> and ~=—s—) and
2 3 4 24 24 24
6 8
and -
~ 12 12 12
Reduce 4 and £ to a commoh denominator. •
Reduce •£> r» a:1d 5 j to fractions of a com. denom.
Reduce 2f, and 4 to fractions of a com. denom.
'Rule II.
If the denominators of two given fractions have a con
mon measure, conceive them to be divided by their greate
common measure ; then multiply the terms of each give
fraction by the quotient arising from the other’s deriominato
Examples.
Reduce £ and f to a common denominator.
TT 7 4 7X5 4x3 35 12.
Here and and and ^
Note. In this last example, and those of the two following rules, tl
forms (Iff!? and are printed only to shew which numbe
'9X5 15X3/
or quotients are used in multiplying the terms of the fractions; but
think it quite needless for the pupil to write down his examples in tl-
way; and I would advise him barely to write down such an examp
as the above, thus: and and 11; and so of others.
9 15 45 45
REDUCTION OTF VULGAR FRACTIONS.
VI. Ti> reduce fractions of different denominators to equivc
lent fractions of a common one.
Rule I.
If the fractions can be conveniently reduced to a comma
denominator, by multiplying or dividing theif terms,
cording to note 6, page 57, proceed by that method ; bi
if not, multiply each numerator continually into all the d«
nominators, except its own, for each new numerator: an
multiply all the denominators together for the common d*
nominator.
Note. It is evident, that in this and several other operations, wh<
any ef the proposed quantities are integers, mixt numbers, or compoui
fractions, they must be reduced by their proper rules, to the form
simple fractions.
Examples.
Reduce |, f, and ^ to a common denominator.
Thus —» —> and ~=—s—) and
2 3 4 24 24 24
6 8
and -
~ 12 12 12
Reduce 4 and £ to a commoh denominator. •
Reduce •£> r» a:1d 5 j to fractions of a com. denom.
Reduce 2f, and 4 to fractions of a com. denom.
'Rule II.
If the denominators of two given fractions have a con
mon measure, conceive them to be divided by their greate
common measure ; then multiply the terms of each give
fraction by the quotient arising from the other’s deriominato
Examples.
Reduce £ and f to a common denominator.
TT 7 4 7X5 4x3 35 12.
Here and and and ^
Note. In this last example, and those of the two following rules, tl
forms (Iff!? and are printed only to shew which numbe
'9X5 15X3/
or quotients are used in multiplying the terms of the fractions; but
think it quite needless for the pupil to write down his examples in tl-
way; and I would advise him barely to write down such an examp
as the above, thus: and and 11; and so of others.
9 15 45 45
Set display mode to:
![]() Universal Viewer |
Universal Viewer | ![]() Mirador |
Large image | Transcription
Mirador |
Large image | Transcription
| Antiquarian books of Scotland > Education > Complete treatise on practical arithmetic and book-keeping > (76) |
|---|
| Permanent URL | https://digital.nls.uk/114434482 |
|---|
| Description | Thousands of printed books from the Antiquarian Books of Scotland collection which dates from 1641 to the 1980s. The collection consists of 14,800 books which were published in Scotland or have a Scottish connection, e.g. through the author, printer or owner. Subjects covered include sport, education, diseases, adventure, occupations, Jacobites, politics and religion. Among the 29 languages represented are English, Gaelic, Italian, French, Russian and Swedish. |
|---|