Download files
Complete book:
Individual page:
Thumbnail gallery: Grid view | List view
SECTION I
All the questions in this Section should be attempted.
Marks
1. With the usual notation for the sides and angles of a triangle
and assuming that
prove that
cosiA=Js±=^). (5)
Calculate the size of the greatest angle of the triangle whose
sides are of lengths 13 in, 19 in, and 22 in. (4)
2. Establish the formula for the distance between the points
(xv yd and (x>, y2). (5)
The vertices of a triangle are the points A (2, 10),
B (—8, —10), and C (4, —1). The internal bisector of
the angle BAC meets BC at D; find the coordinates of D. (5)
AD meets the altitude CF at K; find the coordinates of K. (4)
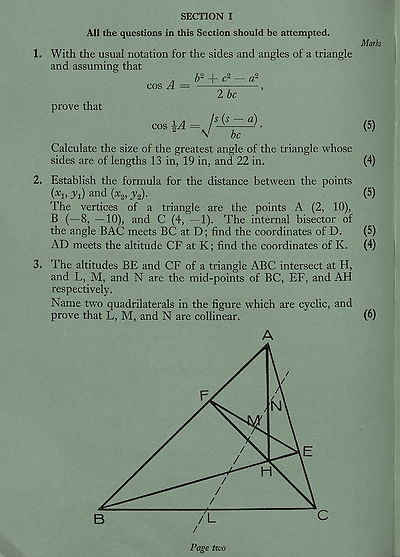
3. The altitudes BE and CF of a triangle ABC intersect at H,
and L, M, and N are the mid-points of BC, EE, and AH
respectively.
Name two quadrilaterals in the figure which are cyclic, and
prove that L, M, and N are collinear. (6)
Page two
All the questions in this Section should be attempted.
Marks
1. With the usual notation for the sides and angles of a triangle
and assuming that
prove that
cosiA=Js±=^). (5)
Calculate the size of the greatest angle of the triangle whose
sides are of lengths 13 in, 19 in, and 22 in. (4)
2. Establish the formula for the distance between the points
(xv yd and (x>, y2). (5)
The vertices of a triangle are the points A (2, 10),
B (—8, —10), and C (4, —1). The internal bisector of
the angle BAC meets BC at D; find the coordinates of D. (5)
AD meets the altitude CF at K; find the coordinates of K. (4)
3. The altitudes BE and CF of a triangle ABC intersect at H,
and L, M, and N are the mid-points of BC, EE, and AH
respectively.
Name two quadrilaterals in the figure which are cyclic, and
prove that L, M, and N are collinear. (6)
Page two
Set display mode to:
Universal Viewer | 
Mirador |
Large image | Transcription
Images and transcriptions on this page, including medium image downloads, may be used under the Creative Commons Attribution 4.0 International Licence unless otherwise stated. 
| Scottish school exams and circulars > Scottish Certificate of Education > 1963 > (90) |
|---|
| Permanent URL | https://digital.nls.uk/130800212 |
|---|---|
More information
|
|
| Attribution and copyright: |
|
|---|---|
|
More information
|
|
| Shelfmark | GEB.16 |
|---|---|
| Additional NLS resources: | |
|
More information
|
|
| Description | Examination papers for the School Leaving Certificate 1888-1961 and the Scottish Certificate of Education 1962-1963. Produced by the Scotch (later 'Scottish') Education Department, these exam papers show how education developed in Scotland over this period, with a growing choice of subjects. Comparing them with current exam papers, there are obvious differences in the content and standards of the questions, and also in the layout and use of language |
|---|---|
| Additional NLS resources: |
|
|
More information
|
|
